第11篇：高级数据类型之集合

基础数据类型：

• int，整数类型（整形）

• float，浮点类型（浮点型）

• complex,复数类型

• bool，布尔类型

• str，字符串类型

高级数据类型

• list，列表类型

• tuple，元组类型

• set，集合类型

• dict，字典类型

学习目标：

掌握集合相关知识。

在学习了列表和元组之后，我们再来学习一种容器型的数据类型，它的名字叫集合（set）。说到集合这个词大家一定不会陌生，在数学课本上就有这个概念。通常我们对集合的定义是“把一定范围的、确定的、可以区别的事物当作一个整体来看待”，

集合中的各个事物通常称为集合的元素。集合应该满足以下特性：

1. 无序性：一个集合中，每个元素的地位都是相同的，元素之间是无序的。
2. 互异性：一个集合中，任何两个元素都认为是不相同的，即每个元素只能出现一次。
3. 确定性：给定一个集合，任给一个元素，该元素或者属于或者不属于该集合，二者必居其一，不允许有模棱两可的情况出现。

Python程序中的集合跟数学上的集合是完全一致的，需要强调的是上面所说的无序性和互异性。

无序性说明集合中的元素并不像列中的元素那样一个挨着一个，可以通过索引的方式实现随机访问（随机访问指的是给定一个有效的范围，随机抽取出一个数字，然后通过这个数字获取到对应的元素），所以Python中的集合肯定不能够支持索引运算。

另外，集合的互异性决定了集合中不能有重复元素，这一点也是集合区别于列表的关键，说得更直白一些就是，Python中的集合类型具有去重特性。

当然，Python中的集合一定是支持in和not in成员运算的，这样就可以确定一个元素是否属于集合，也就是上面所说的集合的确定性。

集合的成员运算在性能上要优于列表的成员运算，这是集合的底层存储特性决定的，此处我们暂时不做讨论，先记下这个结论即可。

一、集合的定义

通过对比列表和元组，我们来看一下集合的定义：

• 列表（list），是一个有序且可变的容器，在里面可以存放多个不同类型、数据元素可重复的元素。

• 元组（tuple），是一个有序且不可变的容器，在里面可以存放多个不同类型、数据元素可重复的元素。

• 集合（set），是一个 无序 且可变的容器，在里面可以存放多个不同类型、数据元素不可重复的元素。

• 集合的特点：

  • 以{}包裹，,为分隔符
  • 内部元素无序：无法通过索引取值
  • 内部元素可变：可以添加和删除元素
  • 内部元素类型可不同
  • 内部元素不可重复：经常应用在有去重需求的场景

• 一般什么时候用集合呢？

就是想要维护一大堆不重复的数据时，就可以用它。比如：做爬虫去网上找图片的链接，为了避免链接重复，可以选择用集合去存储链接地址。

二、集合的创建

在Python中，创建集合可以使用{}字面量语法，{}中需要至少有一个元素，因为没有元素的{}并不是空集合而是一个空字典，我们下一节就会大家介绍字典的知识。当然，也可以使用内置函数set来创建一个集合，准确的说set并不是一个函数，而是创建集合对象的构造器，这个知识点我们很快也会讲到，现在不理解跳过它就可以了。要创建空集合可以使用set()；也可以将其他序列转换成集合，例如：set('hello')会得到一个包含了4个字符的集合（重复的l会被去掉）。除了这两种方式，我们还可以使用生成式语法来创建集合，就像我们之前用生成式创建列表那样。要知道集合中有多少个元素，还是使用内置函数len；使用for循环可以实现对集合元素的遍历。

# 创建集合的字面量语法(重复元素不会出现在集合中)
set1 = {1, 2, 3, 3, 3, 2}
print(set1)         # {1, 2, 3}
print(len(set1))    # 3

# 创建集合的构造器语法(后面会讲到什么是构造器)
set2 = set('hello')
print(set2)         # {'h', 'l', 'o', 'e'}

# 将列表转换成集合(可以去掉列表中的重复元素)
set3 = set([1, 2, 3, 3, 2, 1])
print(set3)         # {1, 2, 3}

# 创建集合的生成式语法(将列表生成式的[]换成{})
set4 = {num for num in range(1, 20) if num % 3 == 0 or num % 5 == 0}
print(set4)         # {3, 5, 6, 9, 10, 12, 15, 18}

# 集合元素的循环遍历
for elem in set4:
    print(elem)

注意：定义空集合时，只能使用v = set()，不能使用 v={}（这样是定义一个空字典）。

v1 = []
v11 = list()

v2 = ()
v22 = tuple()

v3 = set()

v4 = {} # 空字典
v44 = dict()

需要提醒大家，集合中的元素必须是hashable类型。所谓hashable类型指的是能够计算出哈希码的数据类型，你可以暂时将哈希码理解为和变量对应的唯一的ID值。通常不可变类型都是hashable类型，如整数、浮点、字符串、元组等，而可变类型都不是hashable类型，因为可变类型无法确定唯一的ID值，所以也就不能放到集合中。集合本身也是可变类型，所以集合不能够作为集合中的元素，这一点请大家一定要注意。

三、集合的方法

集合常用的方法如下：

• 添加
  • add(value)，在集合中添加一个元素
• 删除
  • pop()，删除并返回任意集合元素，若集合为空，则引发KeyError
  • discard(value)，在集合中删除指定元素，若不存在不报错
  • remove(value)，在集合中删除指定元素，若不存在报错
  • del set，删除集合
• 清空
  • clear()，清空集合
• 求交集
  • intersection(set2)，返回两个集合的交集，自身集合不发生改变
  • intersection_update(set2)，在自身集合的基础上求两个集合的交集，改变自身集合
• 求并集
  • update(set2)，使用自身和其他集合的并集来更新集合，改变自身集合
  • union(set2)，并集，返回两个集合的并集，不改变自身
• 求差集
  • difference(set2)，返回两个集合的差集，自身集合不发生改变
  • difference_update(set2)，在自身集合的基础上求两个集合的差集，改变自身集合
  • symmetric_difference(set2)，对称差集
• 求超集和子集
  • issuperset(set2)，求超集
  • issubset(set2)，求子集

使用示例

# 1，列表去重。
l1 = [1, 2, 1, 2, 3, 4, 5, 6, 6,]
set1 = set(l1)
l2 = list(set1)
print(l2)  # [1, 2, 3, 4, 5, 6]

# 2，集合的增删查。
set1 = set()

# 添加
set1.add("周杰伦")
set1.add("林俊杰")
print(set1)  # {'周杰伦', '林俊杰'}
set2 = {"刘嘉玲", '关之琳', "王祖贤", "张曼⽟", "李若彤"}
set1.update(set2)
print(set1)  # {'王祖贤', '刘嘉玲', '张曼⽟', '周杰伦', '林俊杰', '关之琳', '李若彤'}
print(set1.union(set2))  # # {'王祖贤', '刘嘉玲', '张曼⽟', '周杰伦', '林俊杰', '关之琳', '李若彤'}

# 删除
print(set1.pop()) # 关之琳  随机删除 返回指定元素
print(set1)       # {'周杰伦', '张曼⽟', '李若彤', '王祖贤', '林俊杰', '刘嘉玲'}
set1.remove('刘嘉玲')  # 删除指定元素 若不存在 会引发KeyError异常 {'周杰伦', '张曼⽟', '李若彤', '王祖贤', '林俊杰'}
print(set1)
set1.discard('李若彤')  # 删除指定元素 若不存在不报错
print(set1)          # {'周杰伦', '张曼⽟', '王祖贤', '林俊杰'}

# 清空
# set1.clear()
# print(set1)   # set()
# del set1
# print(set1)   # NameError: name 'set1' is not defined

# 查询: for循环
for val in set1:
    print(val)

# 3，集合的关系测试。
set1 = {1, 2, 3, 4, 5}
set2 = {4, 5, 6, 7, 8}

# 交集：& intersection
print(set1 & set2)       # {4, 5}
print(set1.intersection(set2))  # {4, 5}

# 并集：| union
print(set1 | set2)        # {1, 2, 3, 4, 5, 6, 7, 8}
print(set1.union(set2))   # {1, 2, 3, 4, 5, 6, 7, 8}

# 差集：- difference
print(set1 - set2)            # {1, 2, 3}
print(set1.difference(set2))  # {1, 2, 3}

# 对称差集: ^ symmetric_difference
print(set1 ^ set2)                      # {1, 2, 3, 6, 7, 8}
print(set1.symmetric_difference(set2))  # {1, 2, 3, 6, 7, 8}

set1 = {1, 2, 3, 4, 5}
set2 = {1, 2, 3}

# 超集：>
print(set1 > set2)         # True
print(set1.issuperset(set2)) # True

# 子集：< issubset
print(set2 < set1)         # True
print(set2.issubset(set1))  # True

如果要判断两个集合有没有相同的元素可以使用isdisjoint方法，没有相同元素返回True，否则返回False，代码如下所示。

set1 = {'Java', 'Python', 'Go', 'Kotlin'}
set2 = {'Kotlin', 'Swift', 'Java', 'Objective-C', 'Dart'}
set3 = {'HTML', 'CSS', 'JavaScript'}
print(set1.isdisjoint(set2))    # False
print(set1.isdisjoint(set3))    # True

四、集合的运算

Python为集合类型提供了非常丰富的运算符，主要包括：成员运算、交集运算、并集运算、差集运算、比较运算（相等性、子集、超集）等。常见运算总结如下：

• 成员运算
  • int/not in：检查元素是否在集合中
• 交并差运算
  • &：求两个集合的交集，即公共的元素
  • |：求两个集合的并集，即两个集合中去重之后所有的元素
  • -：求两个集合中的差集，及第一个集合中有第二个集合中没有的元素
  • ^：求两个集合中的对称差，即两个集合的并集减去两个集合的差集
• 比较运算
  • == ：判断两个集合中元素是否相等
  • != ：判断两个集合中元素是否不等
  • <：判断第一个集合是否是第二个集合的真子集
  • <=：断第一个集合是否是第二个集合的子集
  • >：判断第一个集合是否是第二个集合的超集

1.成员运算

可以通过成员运算in和not in检查元素是否在集合中，代码如下所示。

set1 = {11, 12, 13, 14, 15}
print(10 in set1)        # False 
print(15 in set1)        # True
set2 = {'Python', 'Java', 'Go', 'Swift'}
print('Ruby' in set2)    # False
print('Java' in set2)    # True

2. 交并差运算

Python中的集合跟数学上的集合一样，可以进行交集、并集、差集等运算，而且可以通过运算符和方法调用两种方式来进行操作，代码如下所示。

set1 = {1, 2, 3, 4, 5, 6, 7}
set2 = {2, 4, 6, 8, 10}

# 交集
# 方法一: 使用 & 运算符
print(set1 & set2)                # {2, 4, 6}
# 方法二: 使用intersection方法
print(set1.intersection(set2))    # {2, 4, 6}

# 并集
# 方法一: 使用 | 运算符
print(set1 | set2)         # {1, 2, 3, 4, 5, 6, 7, 8, 10}
# 方法二: 使用union方法
print(set1.union(set2))    # {1, 2, 3, 4, 5, 6, 7, 8, 10}

# 差集
# 方法一: 使用 - 运算符
print(set1 - set2)              # {1, 3, 5, 7}
# 方法二: 使用difference方法
print(set1.difference(set2))    # {1, 3, 5, 7}

# 对称差
# 方法一: 使用 ^ 运算符
print(set1 ^ set2)                        # {1, 3, 5, 7, 8, 10}
# 方法二: 使用symmetric_difference方法
print(set1.symmetric_difference(set2))    # {1, 3, 5, 7, 8, 10}
# 方法三: 对称差相当于两个集合的并集减去交集
print((set1 | set2) - (set1 & set2))      # {1, 3, 5, 7, 8, 10}

通过上面的代码可以看出，对两个集合求交集，&运算符和intersection方法的作用是完全相同的，使用运算符的方式更直观而且代码也比较简短。相信大家对交集、并集、差集、对称差这几个概念是比较清楚的，如果没什么印象了可以看看下面的图。

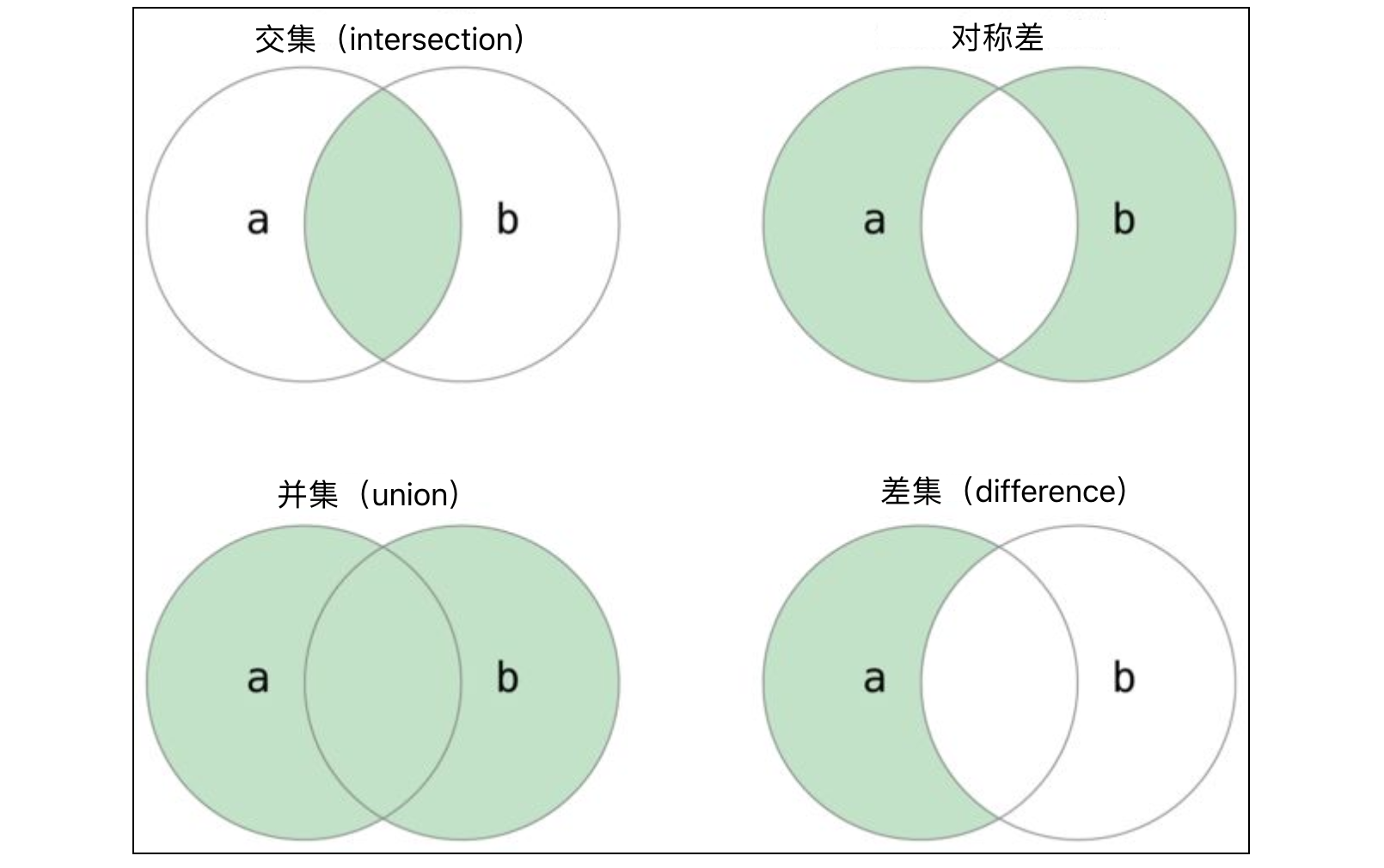
集合的交集、并集、差集运算还可以跟赋值运算一起构成复合运算，如下所示。

set1 = {1, 3, 5, 7}
set2 = {2, 4, 6}
# 将set1和set2求并集再赋值给set1
# 也可以通过set1.update(set2)来实现
set1 |= set2
print(set1)    # {1, 2, 3, 4, 5, 6, 7}
set3 = {3, 6, 9}
# 将set1和set3求交集再赋值给set1
# 也可以通过set1.intersection_update(set3)来实现
set1 &= set3
print(set1)    # {3, 6}

3. 比较运算

两个集合可以用==和!=进行相等性判断，如果两个集合中的元素完全相同，那么==比较的结果就是True，否则就是False。如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集，即对于∀a∈A，均有a∈B，则A⊆B。A是B的子集，反过来也可以称B是A的超集。如果A是B的子集且A不等于B，那么A就是B的真子集。Python为集合类型提供了判断子集和超集的运算符，其实就是我们非常熟悉的<和>运算符，代码如下所示。

set1 = {1, 3, 5}
set2 = {1, 2, 3, 4, 5}
set3 = set2
# <运算符表示真子集，<=运算符表示子集
print(set1 < set2, set1 <= set2)    # True True
print(set2 < set3, set2 <= set3)    # False True
# 通过issubset方法也能进行子集判断
print(set1.issubset(set2))      # True

# 反过来可以用issuperset或>运算符进行超集判断
print(set2.issuperset(set1))    # True
print(set2 > set1)              # True

五、不可变集合

Python中还有一种不可变类型的集合，名字叫frozenset。set跟frozenset的区别就如同list跟tuple的区别，frozenset由于是不可变类型，能够计算出哈希码，因此它可以作为set中的元素。除了不能添加和删除元素，frozenset在其他方面跟set基本是一样的，下面的代码简单的展示了frozenset的用法。

set1 = frozenset({1, 3, 5, 7})
set2 = frozenset(range(1, 6))
print(set1 & set2)    # frozenset({1, 3, 5})
print(set1 | set2)    # frozenset({1, 2, 3, 4, 5, 7})
print(set1 - set2)    # frozenset({7})
print(set1 < set2)    # False

六、集合类型转换

其他类型如果想要转换为集合类型，可以通过set进行转换，并且如果数据有重复自动剔除。

提示：int/list/tuple/dict都可以转换为集合。

v1 = "张亚飞"
v2 = set(v1)
print(v2) # {"张","亚","飞"}

v1 = [11,22,33,11,3,99,22]
v2 = set(v1)
print(v2) # {11,22,33,3,99}

v1 = (11,22,3,11)
v2 = set(v1)
print(v2) # {11,22,3}

提示：这其实也是去重的一个手段。

data = {11,22,33,3,99}
v1 = list(data) # [11,22,33,3,99]
v2 = tuple(data) # (11,22,33,3,99)

七、集合生成式

s = {v for v in iterable} 其中iterable是一个可迭代的对象，比如list。

示例1：求余数

# for in 循环实现
l1 = [3,5,7,8,9,10,20]
s = set()
for i in li:
    s.add(l1 % 3)
print(s) # {0, 1, 2}
# 集合生成式
s = { i % 3 for i in range(1,7)}
print(s) #  {0, 1， 2}

示例2：嵌套if

# for in 循环实现
l1 = [3,5,7,8,9,10,20]
s = set()
for i in li:
    if i < 15:
    	s.add(l1 % 3)
print(s) # {0, 1， 2}
# 集合生成式
s = { i % 3 for i in l1 if i < 15}
print(s) #  {0, 1， 2}

示例3：嵌套循环

# for in 循环
S = set()
for i in range(1,4):
    for j in range(1,4):
        S.add(( i * j))
print(S)  # {1, 2, 3, 4, 6, 9}

# 集合生成式
S = { i*j for i in range(1,4) for j in range(1,4)}
print(s)  # {1, 2, 3, 4, 6, 9}

八、集合的存储原理

1. 元素必须可哈希

因存储原理，集合的元素必须是可哈希的值，即：内部通过通过哈希函数把值转换成一个数字。

目前可哈希的数据类型：int、bool、str、tuple，而list、set是不可哈希的。

总结：集合的元素只能是 int、bool、str、tuple 。

• 转换成功

  v1 = [11,22,33,11,3,99,22]
  v2 = set(v1)
  print(v2) # {11,22,33,3,99}

• 转换失败

  v1 = [11,22,["Michael","eric"],33]
  v2 = set(v1) # 报错 
  print(v2)

2. 查找速度特别快

因存储原理特殊，集合的查找效率非常高（数据量大了才明显）。

• 低

  # 列表存储
  user_list = ["张亚飞","Michael","刘翔"]
  if "Michael" in user_list:
      print("在")
  else:
      print("不在")
  # 元组存储
  user_tuple = ("张亚飞","Michael","刘翔")
  if "Michael" in user_tuple:
      print("在")
  else:
      print("不在")

• 效率高

  user_set = {"张亚飞","Michael","刘翔"}
  if "Michael" in user_set:
      print("在")
  else:
      print("不在")

3. 对比和嵌套

类型	是否可变	是否有序	元素要求	是否可哈希	转换	定义空
list	是	是	无	否	list(其他)	v=[]或v=list()
tuple	否	是	无	是	tuple(其他)	v=()或v=tuple()
set	是	否	可哈希	否	set(其他)	v=set()

data_list = [
    "Michael",
    11,
    (11, 22, 33, {"Michael", "eric"}, 22),
    [11, 22, 33, 22],
    {11, 22, (True, ["中国", "北京"], "沙河"), 33}
]

注意：由于True和False本质上存储的是 1 和 0 ，而集合又不允许重复，所以在整数 0、1和False、True出现在集合中会有如下现象：

v1 = {True, 1}
print(v1)  # {True}

v2 = {1, True}
print(v2)  # {1}

v3 = {0, False}
print(v3)  # {0}

v4 = {False, 0}
print(v4)  # {False}

九、简单的总结

Python中的集合底层使用了哈希存储的方式，使得其具有查找速度快的优势，且其数据元素不可重复，经常应用在需要大量查找和去重的场景下。现阶段大家只需要知道以下几个知识点：

1. 集合，是 无序、不重复、元素必须可哈希、可变的一个容器（子孙元素都必须是可哈希）。
2. 集合的查找速度比较快（底层是基于哈希进行存储）
3. 集合可以具有 交并差 的功能。
4. 不支持索引运算

集合与列表不同的地方在于集合中的元素没有序、不能用索引运算、不能重复。